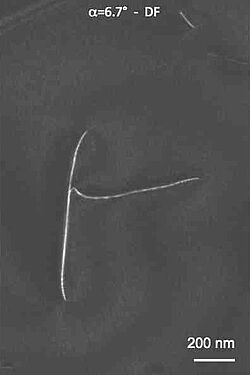Tomographie électronique
Tomographie MET des dislocations
Pour modéliser la déformation plastique par la dynamique des dislocations, il est nécessaire de connaître la géométrie du glissement, c'est-à-dire les plans de glissement, de montée et de glissement dévié, entre autres. Une bonne connaissance de la géométrie des interactions de dislocations est également requise. La tomographie électronique peut être appliquée aux dislocations et donne accès à la véritable structure 3D d'une microstructure de dislocations. Il est possible de reconstruire un objet de petite taille (de plusieurs mm à plusieurs nm) en 3D en utilisant la TEM. La TEM donne accès à des images projetées pour différents angles projetés. Ces séries d'images sont appelées «séries tiltées». La plage angulaire peut atteindre +/- 60 ° pour des pièces polaires espacées et +/- 80 ° pour les porte-échantillons dédiés à la tomographie. Plus la plage angulaire augmente, plus le volume manquant (« missing wedge » en anglais) diminue et plus la qualité du volume de reconstruction augmente. Il existe plusieurs algorithmes de reconstruction, les plus courants étant WBP (weighted back projection) et le SIRT (the simultaneous iterative reconstruction technique). Ils sont capables de transformer une série tiltée en un empilement.
Les distorsions des plans cristallographiques dues aux dislocations sont à l'origine des contrastes de dislocations observés sur les micrographies MET. Ces contrastes sont fortement liés à l'orientation cristalline. Par conséquent, l'échantillon doit être parfaitement orienté de manière à aligner le vecteur de diffraction le long de l'axe d'inclinaison du porte-objet afin d'éviter toutes les variations d'angle de Bragg lors de l'acquisition de la série tiltée (une précision de l'ordre du dixième de degré est nécessaire). De plus, le contraste des images doit être homogène pour obtenir la meilleure qualité de reconstruction 3D. Nous effectuons des acquisitions dans le mode de faisceau-faible en TEM qui donne un rapport signal / bruit élevé. L'association d'une légère précession du faisceau d'électrons assure un contraste homogène. Pour augmenter le contraste des dislocations, après acquisition, il est préférable de filtrer les images de la série tiltée en utilisant par exemple un filtre Kernel et un fit polynomial (Mussi et al., 2014). Dans les images ici, nous montrons une image en mode faisceau-faible champ-sombre (WBDF, weak beam dark field) d'une dislocation à droite et à gauche d'un volume de reconstruction tomographique montrant des plans de glissement et une boucle sessile sur un plan de montée.
Alexandre Mussi (Plasticité-UMET), Patrick Cordier (Plasticité-UMET)

Tomographie en HAADF-STEM d'une roche argileuse naturelle pour une meilleure prédiction du transport des fluides
Cette étude vient dans le prolongement d’un ensemble de publications (Song et al., 2015, Song et al., 2016, Song et al., 2016) visant à caractériser le réseau poreux d’une roche argileuse naturelle par imagerie (méthode directe). Ce réseau s’étend sur plusieurs échelles, de telle façon que seuls 2% de la porosité est présente jusqu’à une taille de pores de l’ordre de la dizaine de nm : il faut descendre à l’échelle nanométrique (<10 nm) pour identifier l’essentiel de la porosité. Nos recherches antérieures ont permis d’identifier ce réseau poreux nanométrique par MET 2D, combiné à un algorithme de reconstruction d’images 3D, qui n’a pas pu être validé expérimentalement.
L’étude développée ici vise à justement caractériser le réseau poreux nanométrique de la roche argileuse naturelle, par STEM tomographique en imagerie HAADF, afin de disposer de données fiables, permettant de compléter et valider expérimentalement les images reconstruites numériquement. A terme, il s’agit de prédire et de comprendre le transport de fluides et de radionucléides au travers de la roche naturelle, dans un contexte où elle est candidate au stockage à long terme de déchets radioactifs.
Catherine Davy (CIMEND-UCCS), Alexandre Mussi (Plasticité-UMET), Maya Marinova (PMEL), Pierre M. Adler (UMR 7619 Metis, Sorbonne University)